Algebraic Starscapes
Support
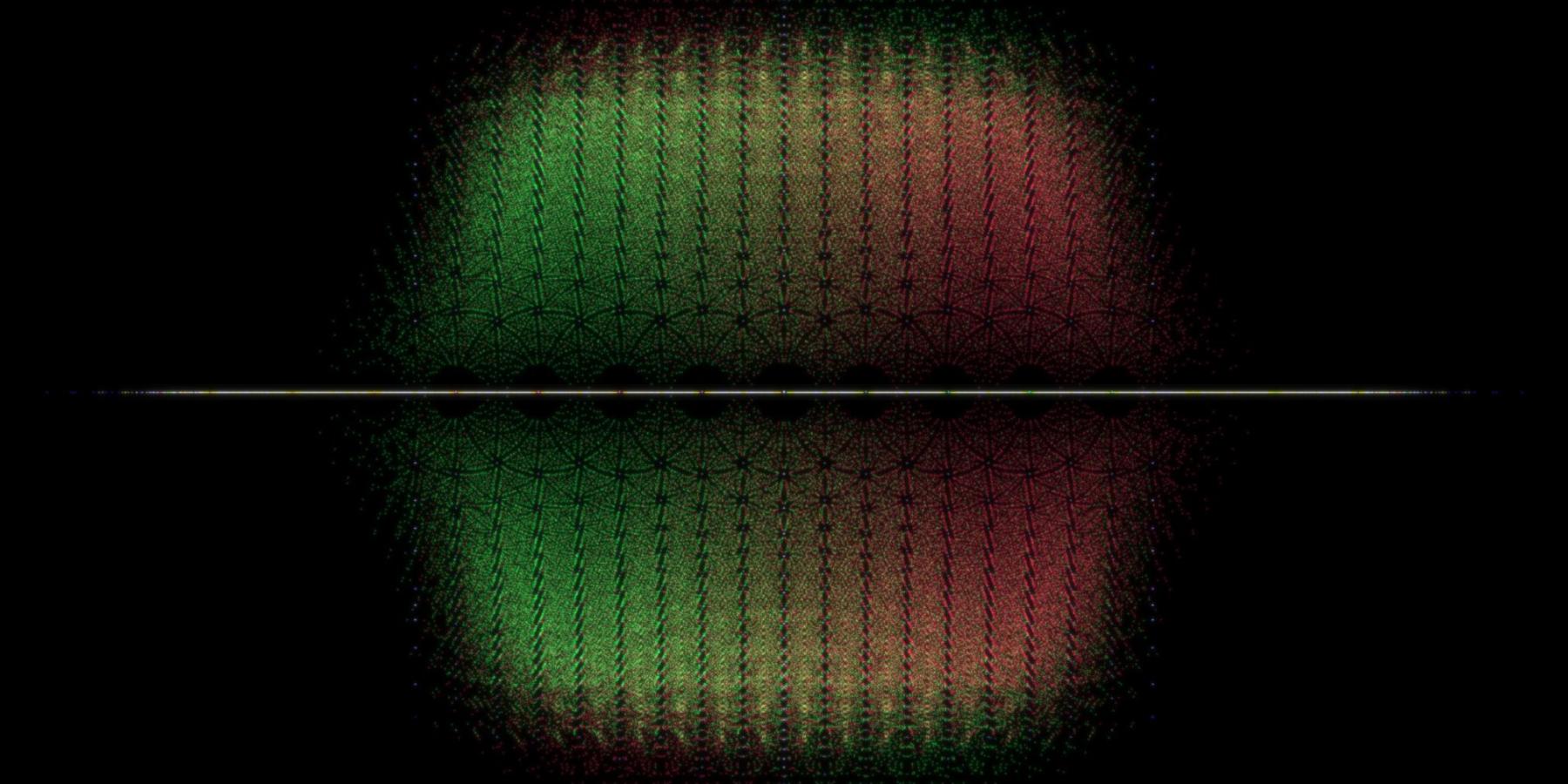
The fundamental theorem of algebra states that every polynomial equation with complex coefficients has complex roots. These roots can be mapped on the complex plane, resulting in beautiful, geometric patterns called algebraic starscapes. I developed python code to compute and graph the complex eigenvalues of specific families of matrices, utilizing St. Lawrence's supercomputer for the millions of computations this required. I experimented with matrix size and integer inputs, as well as a multitude of variables in the graphic generation phase. My final images highlight the effects of an eigenvalue’s associated determinant. The eigenvalue’s pixel color and brightness are modified by its determinant’s sign (positive vs negative) and size (large vs small). I used techniques such as Gaussian blurring and kernel cropping to generate the images. Algebraic starscapes are visual mathematical models. As such, they bridge the divide between math and art. This allows even non-mathematically oriented people to appreciate the beauty of mathematics and open them to conversation about deep mathematical concepts. I intend on continuing this research in the spring as an independent SYE to further analyze my results and generate more advanced images.